A problem that beckoned

During a casual tour of the Web, my attention was drawn to a problem that was stated so simply that it beckoned an attempt at a solution. It was purported to be from a Mathematical Olympiad, which raised its attractiveness index, as such problems are known to strenuously exercise the grey cells, while still retaining the charm of a sport. Only later did I find out that the problem I had written down had omitted an important constraint that made the problem all the more memorable. This is an account of my escapade into the land of mathematics in search of a solution to an intriguing problem.

The problem

The problem, as I first came across it, was posed thus. \[ \text{If}\quad x + xy + y = 54 \qquad{(1)}\] what is \(x + y\)?

If you are good at mathematics, or relish a challenge, do not read further until you have given this problem your very best shot. After that, do read on.

First thoughts

At first, I thought that this problem was too easy to be featured in a Mathematics Olympiad.¹ After all, the problem statement would be intelligible to anyone who has gone through mathematics up to middle (or secondary) school level. But after a short while, I realized that it posed some definite challenges.

In this blog, I am not setting out to expound a blazingly fast method of solution, nor am I attempting mathematical terseness. I will be discursive because I want to savour the problem in all its aspects, as they suggested themselves to me. I also hope that, by so doing, I stimulate mathematical thinking in my readers, and give them an experience of the mathematical adventure, if nothing else.

A pictorial approach

Mathematics may be approached through pictures, or through words, or through a combination of both. Here, I am going to try pictures first. This means graphing the curve defined by Equation 1 and wresting as many insights as possible from that representation.

How do we graph the given curve? And after that, how do we obtain the value of \(x + y\), which is our ultimate goal? Let us see how this approach pans out.

For a start, I am loath to graph curves by hand. So, I went to my favourite graphing destination on the Web, Desmos, to experiment with the given curve. The Desmos Graphing Calculator offers the easiest and laziest route to visualize various curves.

I typed in \(x + xy + y = 54\) into the textbox for the first graph and got what seemed at first sight to be a pair of curves for a rectangular hyperbola of the form \(xy = k\) where \(k\) is some constant (or number).

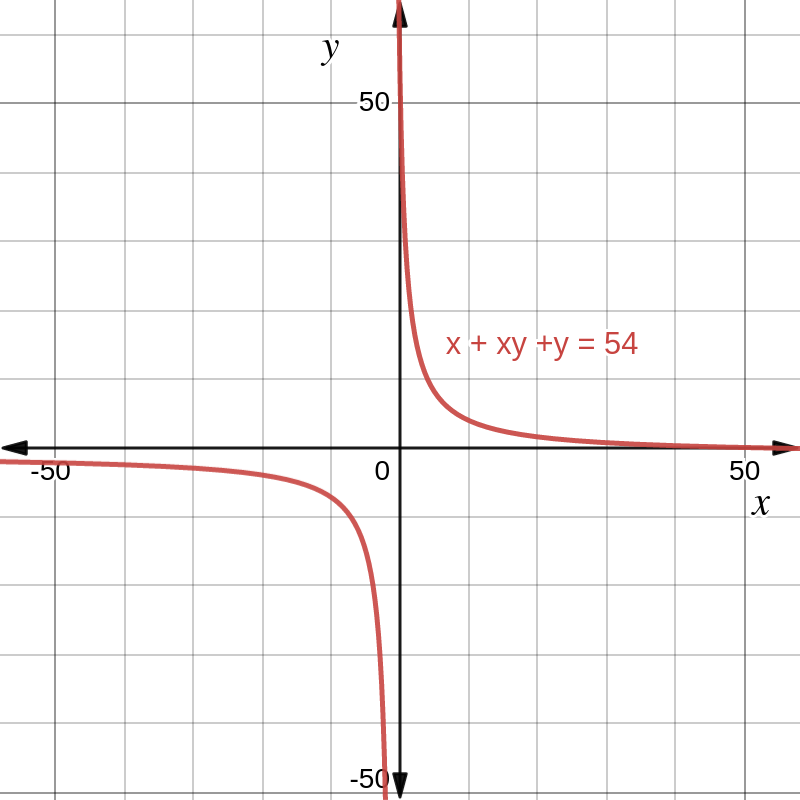
From Figure 1, we can deduce the following:

1. The curve looks like a rectangular hyperbola, with its two portions lying largely in the first and third quadrants.

2. If we re-write Equation 1 to have only \(y\) on the left hand side (LHS), we get: \[ y = \frac{54-x}{x+1} = \frac{54}{x+1} -\frac{x}{x+1} \approx \frac{54}{x} - 1 \approx -1 \; \mbox{for large $x$} \qquad{(2)}\] Wonder no more why the curve resembles a rectangular hyperbola. Its horizontal (and vertical) asymptotes equal \(-1\). That is why it lies largely in the first and third quadrants.

3. Only those points \((x, y)\) that satisfy Equation 1 are relevant for our second condition \(x + y\), i.e., our solution space is defined by the curves comprising the two halves of the plotted graph. The rest of the \(xy\) plane does not contain the solution we seek.

4. Since we are after the value of \(x + y\), we can plot the family of curves \(x + y = k\) where \(k\) is some real constant. This is done in Figure 2. The two straight lines that are tangent can be derived from calculation, as shown in the Appendix at the end. They represent limiting cases of the values of \(k\) within which a solution cannot lie.

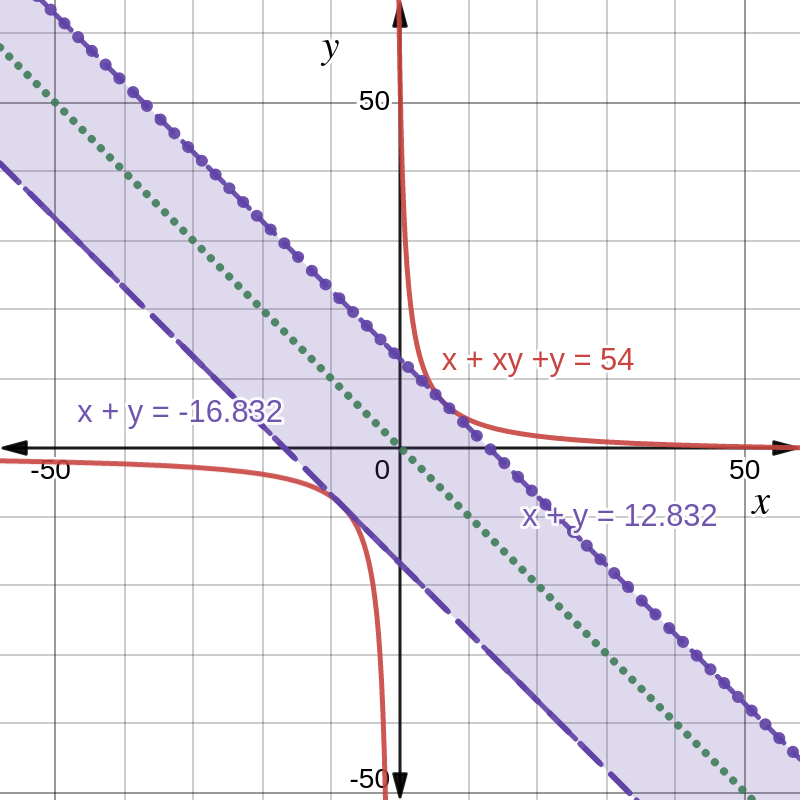
To look for possible solutions, we need to plot straight lines like \(x + y = 20\) and \(x + y = -30\) which will intersect the red curves as shown in Figure 3.

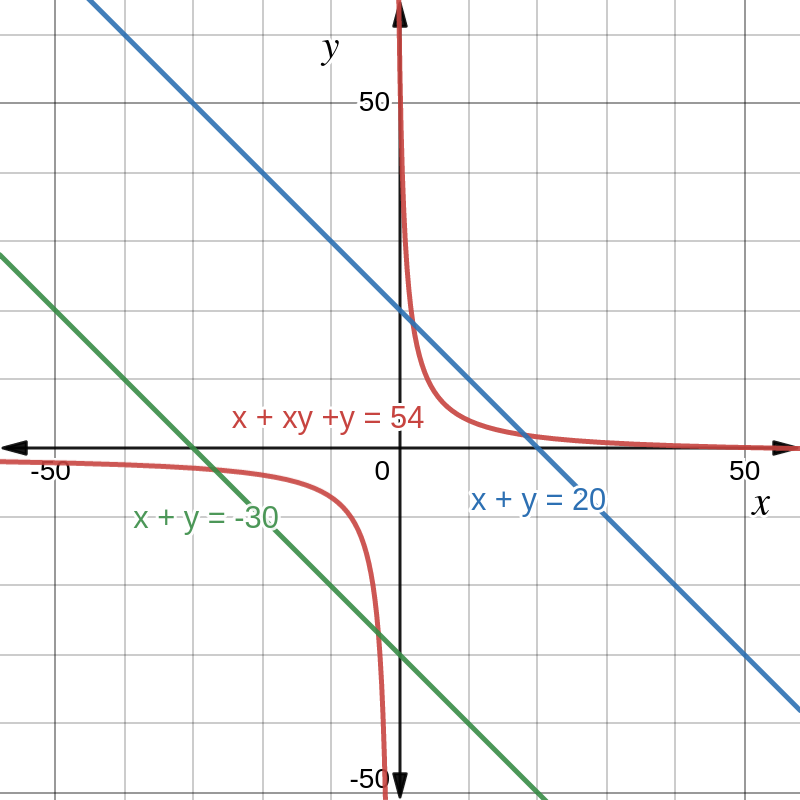
It should be clear that there is nothing special about the numbers \(20\) or \(-30\). So, there is an infinity of possible solutions for \(x + y = k\) in two disjoint sets: \(x + y \geq 12.832\) and \(x + y \leq -16.832\), as shown in the Appendix.

Although we have reached the end of the prescribed quest, there is a sense of hollowness, because there is no unique solution (set), except that the solution can lie anywhere along the red curves, and is forbidden in the purple region of Figure 2.

It is appropriate now to take a breather and re-examine all assumptions. Perhaps, it is the time to ruminate philosophically about mathematical problems.

Mathematics problems and detective novels

Mathematics problems function like detective novels. The author of a detective novel enters into an implicit understanding with the reader, that the clues will be peppered throughout the novel, which when viewed as a whole, will lead to a single culprit, preferably at the end of the novel. If there were still ten possible culprits at the end of the novel, the author would have completely let down the reader’s expectations, and cheated him or her of the reward of discovery for the time spent reading the novel.

A similar compact holds between the one who poses a mathematics problem and the student who is expected to solve it. If a problem has no solutions, or has countless solutions, it will not necessarily enthrall the student, especially at school level. Indeed, it will be considered a breach of faith if either of these two conditions held.

It is unlikely that an Olympiad problem in mathematics will indulge in such antics. What was the exact wording of the problem?

The all-important constraint

A more careful sweep of the Web unearthed a more precise statement of the problem, which included a constraint. For completeness, the problem is re-stated here:

If \(x\) and \(y\) are both positive integers, and \[ x + xy + y = 54 \] what is \(x + y\)?

By restricting the numbers to be positive, we may discard the entire solution set in the fourth quadrant, as well as any solutions that intersect near the (negative-valued) asymptotes. Moreover, by restricting the solution to integers, we are changing the domain of the solution from a quadrant of the Cartesian plane to a point lattice in the first quadrant. The solution set has thus changed from uncountably infinite to countably infinite.

If you observe Figure 3 carefully, when \(k\) is large and positive, the intersection with the given curve will occur near the values of the asymptotes. One way to identify the solution is to vary \(k\) in the straight line \(x + y = k\) by animation, and to identify cases where the intersection occurs at integer values of \(x\) and \(y\). If you are curious how that will look like, go to this animation at the Desmos website to see what happens to the solution as \(k\) varies between \(-30\) and \(30\).

But trying to identify a solution for integers \(x\) and \(y\), by pausing the animation every so often, and looking for whole numbers as the co-ordinates of intersection, will be like yanking a piece of luggage from a fast-moving carousel in an airport. It will be a hit or miss operation rather than a dignified mathematical solution. So, let us switch from the pictorial to the verbal. Let algebra bring to bear its considerable prowess on this problem.

Algebra to the rescue

Let us shuffle the components of Equation 1 in an effort to introduce even more symmetry, and gain a deeper insight: \[ \begin{aligned} x + xy + y &= 54\\ x(1 + y) + y &= 54\; ; \mbox{add one to each side} \\ x(1 + y) + y + 1 &= 55\\ x(y + 1) + (y + 1) &= 55\\ (y + 1)(x + 1) &= 55\\ \end{aligned} \qquad{(3)}\]

Why products over sums?

Take a look at Equation 3. Given that we are asked to evaluate \(x + y\), why did we try to express the number 55 as a product of two numbers on the LHS, rather than as the sum of two numbers?

Decomposing a number \(n\) into a sum of numbers is called additive partitioning, and is represented by the function \(p(n)\), while decomposing a number into a product of numbers is called multiplicative partitioning or unordered factorization and is represented by the expression \(f(n)\) [1].

Consider the number \(6\). We may express it as a sum, using the numbers from \(1\) to \(6\), in eleven different ways, i.e., \(p(6) = 11\). But we may express it in only two different ways as a product, i.e., \(f(n)=2\). Note that we we are talking of distinct decompositions.

It is tempting to speculate that for any positive integer \(n\), \(p(n) \geq f(n)\), but I have not seen any proof of this statement. For our purposes though, it is patently reasonable² to claim that the number of ways in which the number \(55\) may be decomposed as a product is far fewer than the number of ways in which it can be decomposed as a sum, i.e., \(f(n) < p(n)\). And that is why we sought to write the LHS of the last line of Equation 3 as a product rather than as a sum.

Multiplicative partitions of \(55\)

The number 55 may be decomposed into these four unique factors—meaning that order does not matter: \(1, 5, 11,\) and \(55\)³. The fact that \(5\) and \(11\) are prime numbers and that their product is \(55\) has helped whittle down the number of factors.

Let us examine the possible solutions, one by one. If we assign the number \(1\) to \(x + 1\), then \(x\) must be zero. But we have been told that \(x\) and \(y\) are both positive integers, meaning that they cannot be zero or negative. So, the factor-pair \(1\) and \(55\) is not valid.

We may now write Equation 3 as: \[ (x+1)(y+1) = 55 = 5\times 11 \qquad{(4)}\] If we set \(x + 1 = 5\), we get \(x = 4\). Likewise, setting \(y + 1 = 11\) gives \(y = 10\). Therefore, \(x + y = 4 + 10 = 14\). It should be abundantly clear that \(x\) and \(y\) could interchange their values but their sum will still be the same. So, the solution to the problem is \(x + y = 14\), and we are home and dry.

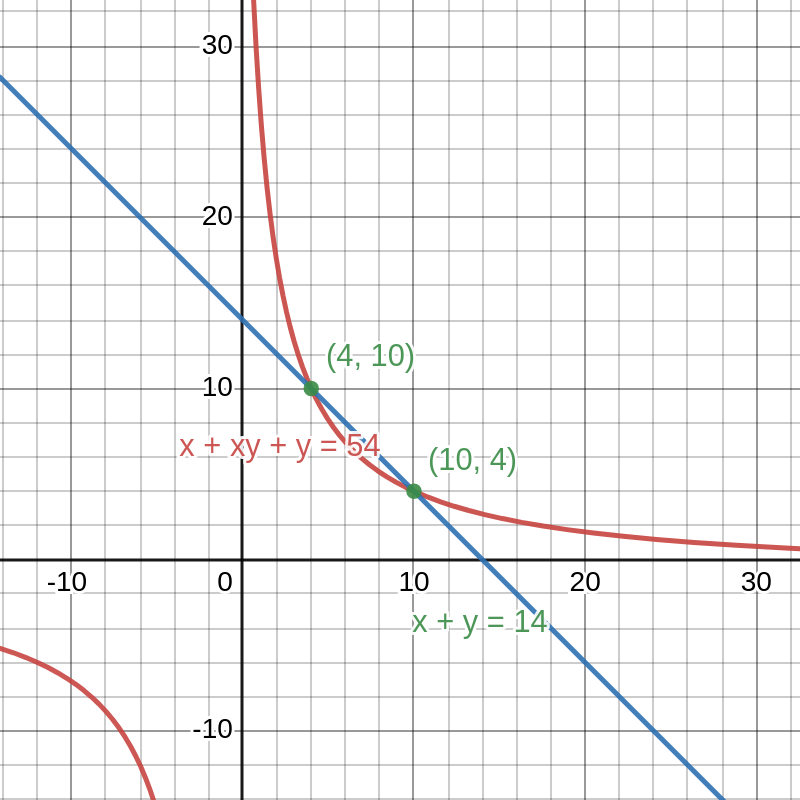
The final picture

To get a sense of finality, let us see the graphical representation of our algebraic result in Figure 4 below.

Appendix

The somewhat magic numbers \(12.832\) and \(-16.832\) in Figure 2 were not drawn out of thin air, but are the result of simple calculations. It should be clear that the straight lines in Figure 2 all have a gradient of \(-1\) and that when they are tangent to—or just touching—the given curve \(x + xy + y = 54\), that curve should also have a gradient of \(-1\) at the point of contact, or osculation.

Rewriting the given equation as \[ y = \frac{54-x}{x+1} \qquad{(5)}\] we want the derivative \(\frac{\mathrm{d}y}{\mathrm{d}x}\). This is accomplished with little effort or thinking, by going to Wolfram Alpha, and asking the engine to compute the derivative so: \[ \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{\mathrm{d}}{\mathrm{d}x}\left[\frac{54 - x}{x + 1}\right] = -\frac{55}{(x + 1)^2} \]

The points at which the gradient is \(-1\) will be those satisfying \[ \begin{aligned} -\frac{55}{(x+1)^2} &= -1 \; \mbox{which gives}\\ x &= \pm\sqrt{55} - 1 \; \mbox{i.e.,}\\ x &\approx 6.416 \;\mbox{and}\; -8.416 \end{aligned} \] The corresponding \(y\) values may be deduced from symmetry, or calculated from Equation 5, to be 6.416, and -8.416 respectively. The two tangents therefore touch the given curve at (6.416, 6.416) and (-8.416, -8.416) and that is why those two tangents that define the solution space were selected for Figure 2. Note that the tangents obey \(x + y = k\) and the two values of \(k\) are \(6.416 + 6.416 = 12.832\), and \(-8.416 + (-8.416) = -16.832\).

Therefore all lines with \(x + y \geq 12.832\) and \(x + y \leq -16.832\) will intersect the given curve and those points of intersection will constitute the solution set for the problem, as originally stated.

Acknowledgements

The Desmos webiste is a boon to both teachers and students of mathematics, not to mention digital artists. YouTube and the rest of the Web contain information on the full extent of the largess available. My grateful thanks to Desmos.

I would also like to express my appreciation to Wolfram Alpha for the computational facilities they have made available at no charge. Much tedium may be avoided, and many insights gained therefrom.

Feedback

Please email me your comments and corrections.

A PDF version of this article is available for download here:

References

•  equation (1)
•  graph (1)
•  IMO (International Mathematical Olympiad) (1)
•  Mathematics (2)
•  number theory (1)